Math ModInt 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 template <int MOD>struct ModInt { unsigned x; ModInt () : x (0 ) { } ModInt (signed sig) : x (sig) { } ModInt (signed long long sig) : x (sig% MOD) { } int get () const return (int )x; } ModInt pow (long long p) { ModInt res = 1 , a = *this ; while (p) { if (p & 1 ) res *= a; a *= a; p >>= 1 ; } return res; } ModInt& operator +=(ModInt that) { if ((x += that.x) >= MOD) x -= MOD; return *this ; } ModInt& operator -=(ModInt that) { if ((x += MOD - that.x) >= MOD) x -= MOD; return *this ; } ModInt& operator *=(ModInt that) { x = (unsigned long long )x * that.x % MOD; return *this ; } ModInt& operator /=(ModInt that) { return (*this ) *= that.pow (MOD - 2 ); } ModInt operator +(ModInt that) const { return ModInt (*this ) += that; } ModInt operator -(ModInt that) const { return ModInt (*this ) -= that; } ModInt operator *(ModInt that) const { return ModInt (*this ) *= that; } ModInt operator /(ModInt that) const { return ModInt (*this ) /= that; } bool operator <(ModInt that) const { return x < that.x; } friend ostream& operator <<(ostream& os, ModInt a) { os << a.x; return os; } };
Frac 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 template <class T >struct Frac { T num; T den; Frac (T num_, T den_) : num (num_), den (den_) { if (den < 0 ) { den = -den; num = -num; } } Frac () : Frac (0 , 1 ) {} Frac (T num_) : Frac (num_, 1 ) {} explicit operator double () const return 1. * num / den; } Frac &operator +=(const Frac &rhs) { num = num * rhs.den + rhs.num * den; den *= rhs.den; return *this ; } Frac &operator -=(const Frac &rhs) { num = num * rhs.den - rhs.num * den; den *= rhs.den; return *this ; } Frac &operator *=(const Frac &rhs) { num *= rhs.num; den *= rhs.den; return *this ; } Frac &operator /=(const Frac &rhs) { num *= rhs.den; den *= rhs.num; if (den < 0 ) { num = -num; den = -den; } return *this ; } friend Frac operator +(Frac lhs, const Frac &rhs) { return lhs += rhs; } friend Frac operator -(Frac lhs, const Frac &rhs) { return lhs -= rhs; } friend Frac operator *(Frac lhs, const Frac &rhs) { return lhs *= rhs; } friend Frac operator /(Frac lhs, const Frac &rhs) { return lhs /= rhs; } friend Frac operator -(const Frac &a) { return Frac (-a.num, a.den); } friend bool operator ==(const Frac &lhs, const Frac &rhs) { return lhs.num * rhs.den == rhs.num * lhs.den; } friend bool operator !=(const Frac &lhs, const Frac &rhs) { return lhs.num * rhs.den != rhs.num * lhs.den; } friend bool operator <(const Frac &lhs, const Frac &rhs) { return lhs.num * rhs.den < rhs.num * lhs.den; } friend bool operator >(const Frac &lhs, const Frac &rhs) { return lhs.num * rhs.den > rhs.num * lhs.den; } friend bool operator <=(const Frac &lhs, const Frac &rhs) { return lhs.num * rhs.den <= rhs.num * lhs.den; } friend bool operator >=(const Frac &lhs, const Frac &rhs) { return lhs.num * rhs.den >= rhs.num * lhs.den; } friend std::ostream &operator <<(std::ostream &os, Frac x) { T g = std::gcd (x.num, x.den); if (x.den == g) { return os << x.num / g; } else { return os << x.num / g << "/" << x.den / g; } } };
Quick power 1 2 3 4 5 6 7 8 9 10 11 12 long long quick_power (long long a, long long b, long long p) a %= p; long long res = 1 ; while (b){ if (b & 1 ){ res = res * a % p; } a = a * a % p; b >>= 1 ; } return res; }
Mat 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 template <class T , int N>struct mat { array<array<T, N>, N> val; mat (){ for (int i = 0 ; i < N; i++){ for (int j = 0 ; j < N; j++){ val[i][j] = 0 ; } } } mat<T, N> operator %=(const long long & p){ for (int i = 0 ; i < N; i++){ for (int j = 0 ; j < N; j++){ val[i][j] %= p; } } return *this ; } };
Multiply 1 2 3 4 5 6 7 8 9 10 11 12 template <class T, int N>mat<T, N> multiply (const mat<T, N>& lm, const mat<T, N>& rm, long long p) { mat<T, N> res; for (int i = 0 ; i < N; i++){ for (int j = 0 ; j < N; j++){ for (int k = 0 ; k < N; k++){ res.val[i][j] = (res.val[i][j] + lm.val[i][k] * rm.val[k][j]) % p; } } } return res; }
Quick power 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 template <class T, int N>mat<T, N> quick_power (mat<T, N> a, long long b, long long p) { a %= p; mat<T, N> res; for (int i = 0 ; i < N; i++){ res.val[i][i] = 1 ; } while (b){ if (b & 1 ){ res = multiply (res, a, p); } a = multiply (a, a, p); b >>= 1 ; } return res; }
Linear sieves sieve primes 每个质数被其最小的因子删除
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 vector<int > linear_sieves (int n) { vector<int > res; vector<int > vis (n + 1 ) ; for (long long i = 2 ; i <= n; i++){ if (!vis[i]){ res.push_back (i); } for (long long j = 0 ; j < res.size () && i * res[j] <= n; j++){ vis[i * res[j]] = true ; if (i % res[j] == 0 ){ break ; } } } return res; }
sieve divisors
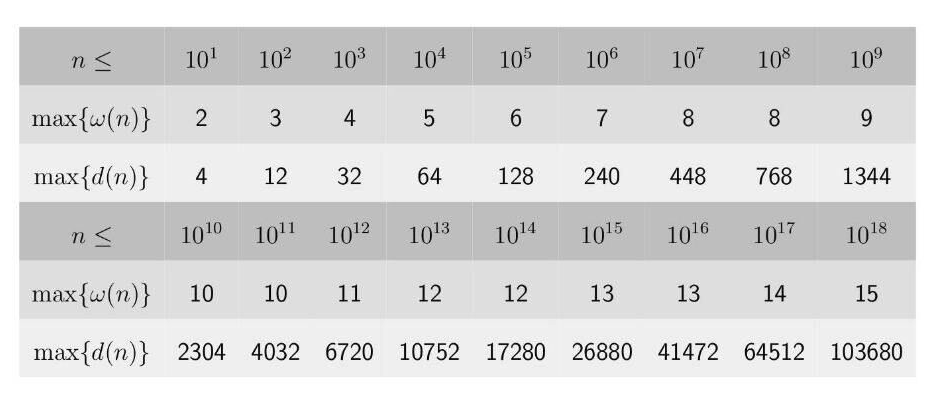
$w(n)$ 表示质因子最多的个数
$d(n)$ 表示约数最多的个数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 struct Divisor { vector<int > p, v; Divisor (int n) { v.resize (n); for (long long i = 2 ; i < n; i++) { if (!v[i]) { v[i] = i; p.push_back (i); } for (int j = 0 ; j < p.size () && i * p[j] < n; j++) { v[i * p[j]] = p[j]; if (i % p[j] == 0 ) { break ; } } } } auto get (int x) const vector<int > div (1 , 1 ) ; while (x > 1 ) { int l = 0 ; int r = div.size (); int d = v[x]; while (x % d == 0 ) { for (int i = l; i < r; i++) { div.push_back (div[i] * d); } x /= d; l = r; r = div.size (); } } return div; } };
sieve count of divisors $$
$$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 vector<int > sieve_divisors (int n) { vector<int > primes; vector<int > cnt (n + 1 , 1 ) , p (n + 1 ) , vis (n + 1 ) ; for (long long i = 2 ; i <= n; i++) { if (!vis[i]) { primes.push_back (i); cnt[i] = 2 ; p[i] = 1 ; } for (int j = 0 ; j < primes.size () && i * primes[j] <= n; j++) { int val = i * primes[j]; vis[val] = true ; if (i % primes[j] == 0 ) { p[val] = p[i] + 1 ; cnt[val] = cnt[i] / (p[i] + 1 ) * (p[val] + 1 ); break ; } else { p[val] = 1 ; cnt[val] = cnt[i] * (p[val] + 1 ); } } } return cnt; }
sieve sum of divisors $$
Exgcd 1 2 3 4 5 6 7 8 9 10 11 long long Exgcd (long long a, long long b, long long & x, long long & y) if (!b) { x = 1 ; y = 0 ; return a; } long long c = Exgcd (b, a % b, y, x); y -= (a / b) * x; return c; }
Manhattan distance & Chebyshev distance $$
$$
$$
$$
$$
$$
trick
Integral Simpson $$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 const long double eps = 1e-9 ;long double f (long double x) return ; } long double simpon (long double l, long double r) return (f (l) + f (r) + f ((l + r) / 2 ) * 4 ) * (r - l) / 6 ; } long double get (long double l, long double r, long double ans) long double m = (l + r) / 2 ; long double lv = simpon (l, m); long double rv = simpon (m, r); if (fabsl (lv + rv - ans) < eps){ return ans; } return get (l, m, lv) + get (m, r, rv); }; get (l, r, simpon (l, r));