Number theory
Number theory
Inverse
$ax \equiv 1$ $(mod \quad n)$
逆元存在的充要条件 $gcd(a, n) = 1$
$n$ 是质数且 $gcd(a, n) = 1$,逆元 $x \equiv a^{n - 2} \quad (mod \quad n)$ (费马小定理)
$ax + ny = gcd(a, n)$,$gcd(a, n) = 1$ ,求 $x$ 的最小正整数解 (
Exgcd求解)线性递推 $1,2,\cdots,n$ 的逆元:$inv_{i} = (p - \lfloor \frac{p}{i} \rfloor ) \times inv_{p ; mod ; i} \quad mod ; p$
1 | inv[1] = 1; |
- 计算任意 $n$ 个数的逆元,先求前缀积 $S_{n}$ ,对 $S_{n}$ 利用 1 或 2 求解 $S_{n}$ 的逆元 $InvS_{n}$ ,则 $a_{n}$ 的逆元为 $InvS_{n} \times S_{n - 1}$, $InvS_{n - 1} = InvS_{n} \times a_{n}$ 递推即可
1 | s[0] = 1; |
Exgcd
$$
ax + by = gcd(a, b)
$$
求可行解 $x_{0}$ ,$y_{0}$ ,以下为通解
$$
x = x_{0} + \frac{b}{gcd(a, b)} k \
y = y_{0} - \frac{a}{gcd(a, b)} k
$$
1 | long long Exgcd(long long a, long long b, long long& x, long long& y) { |
Bézout’s Lemma
裴蜀定理
$$
ax + by = m
$$
有解的充要条件 $gcd(a, b) \mid m$
通解可利用 Exgcd 求
$$
x = (x_{0} + \frac{b}{gcd(a, b)} k) \frac{m}{gcd(a, b)} \
y = (y_{0} - \frac{a}{gcd(a, b)} k) \frac{m}{gcd(a, b)}
$$
Fermat’s little theorem
费马小定理
$p$ 为质数且 $gcd(a, p) = 1$ ,则 $a^{p - 1} \equiv 1 \quad (mod \quad p)$
求逆元 $ax \equiv 1 \quad (mod \quad p)$
$a \times a^{p - 2} \equiv 1 \quad (mod \quad p) \Rightarrow x \equiv a^{p - 2} \quad (mod \quad p)$
Euler’s function
$$
\varphi(n) = n \times \prod\limits_{i = 1}^{k} \frac{p_{i} - 1}{p_{i}}
$$
质因数分解计算 $O(\sqrt{n})$
1 | long long phi(long long x) { |
可用 Pollard Rho 算法优化。
$$
gcd(a, p) = 1 \Rightarrow a^{\varphi(p)} \equiv 1 \quad (mod \quad p)
$$
$n$ 的所有约数的欧拉函数值之和为 $n$
$$
\sum_{d \mid n} \varphi(d) = n
$$
trick
求 $a_{1}^{a_{2}^{\cdots}} ; % ; p $ 的值,可以递归求解,注意扩展欧拉定理的适用范围,最多进行 $\log$ 次,$\varphi(p)$ 就会变为 1,
1 | // 查询一个区间的答案 [l, r],现预处理 phi 的值 |
Euler’s theorem
若 $gcd(a, p) = 1$ ,则 $a^{\varphi(p)} \equiv 1 \quad (mod \quad p) $ ($\varphi(x)$ 表示 $1$ 到 $x$ 与 $x$ 互质的数的个数)
扩展欧拉定理
$$
a^{b} \equiv
\begin{cases}
a^{b ; mod ; \varphi(p)} & gcd(a, p) = 1 \
a^{b} & gcd(a, p) \neq 1, b < \varphi(p) \
a^{(b ; mod ; \varphi(p)) + \varphi(p)} & gcd(a, p) \neq 1, b \ge \varphi(p)
\end{cases}
\quad (mod \quad p)
$$
Wilson
$(p - 1)! \equiv -1 \quad(mod \quad p)$ 是 $p$ 为质数的充分必要条件
Legendre
$n!$ 中含有的素数 $p$ 的幂次 $v_p(n!)$ 为 $\sum\limits_{i = 1}^{\infty} \lfloor \frac{n}{p^{i}} \rfloor = \frac{n - S_{p}(n)}{p - 1}$ ($S_{p}(n)$ 表示 $n$ 在 $p$ 进制下的各位数的和)
1 | int multiplicity_factorial(int n, int p) { |
Kummer
素数 $p$ 在组合数 $\dbinom{n}{m}$ 中的幂次,恰好是 $p$ 进制下 $m$ 减掉 $n$ 需要借位的次数。
$$
v_p\left(\dbinom{n}{m}\right)=\frac{S_p(m)+S_p(n-m)-S_p(n)}{p-1}
$$
($S_{p}(n)$ 表示 $n$ 在 $p$ 进制下的各位数的和)
Lucas
Lucas 定理内容如下:对于质数 $p$,有
$$
\binom{n}{m}\bmod p = \binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}\cdot\binom{n\bmod p}{m\bmod p}\bmod p
$$
观察上述表达式,可知 $n\bmod p$ 和 $m\bmod p$ 一定是小于 $p$ 的数,可以直接求解,$\displaystyle\binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}$ 可以继续用 Lucas 定理求解。这也就要求 $p$ 的范围不能够太大,一般在 $10^5$ 左右。边界条件:当 $m=0$ 的时候,返回 $1$。
时间复杂度为 $O(f(p) + g(n)\log n)$,其中 $f(n)$ 为预处理组合数的复杂度,$g(n)$ 为单次求组合数的复杂度。
1 | long long lucas(long long n, long long m) { |
exlucas
模数是个合数,
1 | // to do |
ExCrt
给定 $n$ 组非负整数 $a_i, b_i$ ,求解关于 $x$ 的方程组的最小非负整数解。
$$
\begin{cases}
x\equiv b_1\pmod{a_1}\
x\equiv b_2\pmod{a_2}\
\dots\
x\equiv b_n\pmod{a_n}
\end{cases}
$$
采用裴蜀定理计算求得通解,逐个合并求解,通解:$x_{0} + k \times mod$
设两个方程分别是 $x\equiv a_1 \pmod {m_1}$、$x\equiv a_2 \pmod {m_2}$;
将它们转化为不定方程:$x=m_1p+a_1=m_2q+a_2$,其中 $p, q$ 是整数,则有 $m_1p-m_2q=a_2-a_1$。
由裴蜀定理,当 $a_2-a_1$ 不能被 $\gcd(m_1,m_2)$ 整除时,无解;
其他情况下,可以通过扩展欧几里得算法解出来一组可行解 $(p, q)$;
则原来的两方程组成的模方程组的解为 $x\equiv b\pmod M$,其中 $b=m_1p+a_1$,$M=\text{lcm}(m_1, m_2)$。
多个方程用上面的方法两两合并即可。
1 | template<class T = __int128_t> |
ExBSGS
求满足 $a^{x} \equiv b \quad (mod \quad p)$ 的最小非负整数解
考虑分块 $x = i \times m - j$ 先枚举 $j$ 把结果放到哈希表中,再枚举 $i$ 查找结果( $m = \sqrt{p}$ )
$a < m, b < m$ 不满足就先 $mod$ 一下。
对 $a,b,m\in\mathbf{Z}^+$,求解
$$
a^x\equiv b\pmod m
$$
其中 $a,m$ 不一定互质。
当 $(a, m)=1$ 时,在模 $m$ 意义下 $a$ 存在逆元,因此可以使用 BSGS 算法求解。于是我们想办法让他们变得互质。
具体地,设 $d_1=(a, m)$. 如果 $d_1\nmid b$,则原方程无解。否则我们把方程同时除以 $d_1$,得到
$$
\frac{a}{d_1}\cdot a^{x-1}\equiv \frac{b}{d_1}\pmod{\frac{m}{d_1}}
$$
如果 $a$ 和 $\frac{m}{d_1}$ 仍不互质就再除,设 $d_2=\left(a, \frac{m}{d_1}\right)$. 如果 $d_2\nmid \frac{b}{d_1}$,则方程无解;否则同时除以 $d_2$ 得到
$$
\frac{a^2}{d_1d_2}\cdot a^{x-2}≡\frac{b}{d_1d_2} \pmod{\frac{m}{d_1d_2}}
$$
同理,这样不停的判断下去,直到 $a\perp \dfrac{m}{d_1d_2\cdots d_k}$.
记 $D=\prod_{i=1}^kd_i$,于是方程就变成了这样:
$$
\frac{a^k}{D}\cdot a^{x-k}\equiv\frac{b}{D} \pmod{\frac{m}{D}}
$$
由于 $a\perp\dfrac{m}{D}$,于是推出 $\dfrac{a^k}{D}\perp \dfrac{m}{D}$. 这样 $\dfrac{a^k}{D}$ 就有逆元了,于是把它丢到方程右边,这就是一个普通的 BSGS 问题了,于是求解 $x-k$ 后再加上 $k$ 就是原方程的解啦。
注意,不排除解小于等于 $k$ 的情况,所以在消因子之前做一下 $\Theta(k)$ 枚举,直接验证 $a^i\equiv b \pmod m$,这样就能避免这种情况。
1 | template<class T = long long> |
BSGS
1 | long long quick_power(long long a, long long b, long long p){ |
Primitive-root
满足同余式 $a^n \equiv 1 \pmod m$ 的最小正整数 $n$ 存在,这个 $n$ 称作 $a$ 模 $m$ 的阶,记作 $\delta_m(a)$ 或 $\operatorname{ord}_m(a)$.
性质
- $a,a^2,\cdots,a^{\delta_m(a)}$ 模 $m$ 两两不同余。
- 若 $a^n \equiv 1 \pmod m$,则 $\delta_m(a)\mid n$.
- 设 $m\in\mathbf{N}^{*}$,$a,b\in\mathbf{Z}$,$(a,m)=(b,m)=1$,则 $\delta_m(ab)=\delta_m(a)\delta_m(b)$ 的充分必要条件是 $\left(\delta_m(a), \delta_m(b)\right)=1$
- 设 $k \in \mathbf{N}$,$m\in \mathbf{N}^{*}$,$a\in\mathbf{Z}$,$(a,m)=1$,则 $\delta_m(a^k)=\dfrac{\delta_m(a)}{\left(\delta_m(a),k\right)}$
设 $m \in \mathbf{N}^{}$,$g\in \mathbf{Z}$. 若 $(g,m)=1$,且 $\delta_m(g)=\varphi(m)$,则称 $g$ 为模 $m$ 的原根。
即 $g$ 满足 $\delta_m(g) = \left| \mathbf{Z}_m^ \right| = \varphi(m)$. 当 $m$ 是质数时,我们有 $g^i \bmod m,,0 \lt i \lt m$ 的结果互不相同。
原根判定定理
设 $m \geqslant 3, (g,m)=1$,则 $g$ 是模 $m$ 的原根的充要条件是,对于 $\varphi(m)$ 的每个素因数 $p$,都有 $g^{\frac{\varphi(m)}{p}}\not\equiv 1\pmod m$.
1 | // 如果有原根,在 p^0.25 就能找到 复杂度 (p^0.25 * log(phi(p))) 最小原根 |
原根存在定理
一个数 $m$ 存在原根当且仅当 $m=2,4,p^{\alpha},2p^{\alpha}$,其中 $p$ 为奇素数,$\alpha\in \mathbf{N}^{*}$.
1 | // 判断 [0, n] 内的数有无 primitive root (n >= 4) |
原根个数
若一个数 $m$ 有原根,则它原根的个数为 $\varphi(\varphi(m))$.
1 | // phi(p) * log(p) 时间算所有原根 最小原根 g ,所有原根 g^k % p (gcd(k, phi(p)) == 1) |
Sqrt-decomposition
引理
$$
\forall a,b,c\in\mathbb{Z},\left\lfloor\frac{a}{bc}\right\rfloor=\left\lfloor\frac{\left\lfloor\frac{a}{b}\right\rfloor}{c}\right\rfloor
$$
结论
对于常数 $n$,使得式子
$$
\left\lfloor\dfrac ni\right\rfloor=\left\lfloor\dfrac nj\right\rfloor
$$
成立且满足 $i\leq j\leq n$ 的 $j$ 值最大为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$,即值 $\left\lfloor\dfrac ni\right\rfloor$ 所在块的右端点为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$。
($i$ 不是第几块,而是下标)
向上取整
向上取整与前文所述的向下取整十分类似,但略有区别:
对于常数 $n$,使得式子
$$
\left\lceil\dfrac ni\right\rceil=\left\lceil\dfrac nj\right\rceil
$$
成立且满足 $i\leq j\leq n$ 的 $j$ 值最大为 $\left\lfloor\dfrac{n-1}{\lfloor\frac{n-1}i\rfloor}\right\rfloor$,即值 $\left\lceil\dfrac ni\right\rceil$ 所在块的右端点为 $\left\lfloor\dfrac{n-1}{\lfloor\frac{n-1}i\rfloor}\right\rfloor$。
当 $i=n$ 时,上式会出现分母为 $0$ 的错误,需要特殊处理。
证明:$\left\lceil\dfrac ni\right\rceil=\left\lfloor\dfrac{n-1}i\right\rfloor+1$,可以发现 $n$ 的上取整分块与 $n-1$ 的下取整分块是一样的。
Mobius
$$
f(n) = \sum\limits_{d \mid n} g(d) \
g(n) = \sum\limits_{d \mid n} \mu(d) f(\frac{n}{d})
$$
数论函数 $f(n)$ 称为数论函数 $g(n)$ 的莫比乌斯变换
数论函数 $g(n)$ 称为数论函数 $f(n)$ 的莫比乌斯逆变换(反演)
反演结论:
$$
\sum\limits_{d \mid gcd(i, j)} \mu(d) = [gcd(i, j) = 1]
$$
Linear sieves
sieve primes
每个质数被其最小的因子删除
1 | // [2, n] 内的质数 |
sieve divisors
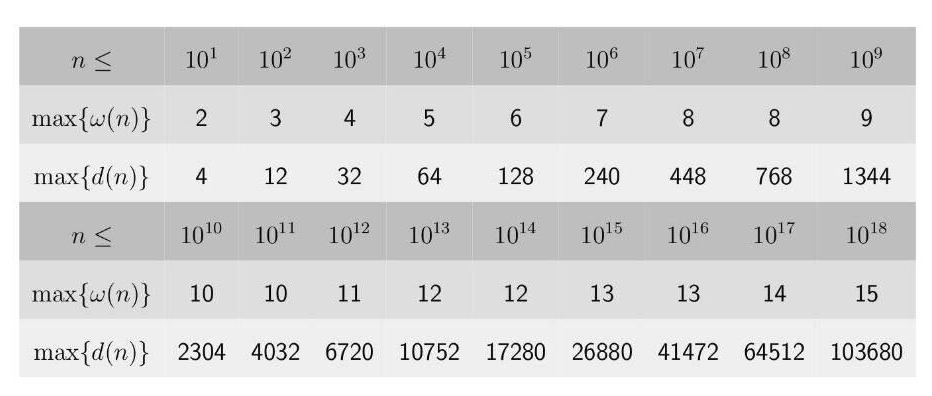
$w(n)$ 表示质因子最多的个数
$d(n)$ 表示约数最多的个数
1 | // 求 [0, n) 某个数的约数 |
sieve count of divisors
$$
唯一分解定理 \quad x = \prod_{i = 1}^{n} p_{i}^{k_{i}} \quad
$$
$$
乘法原理 \quad 约数个数 = \prod_{i = 1}^{n}(k_{i} + 1)
$$
1 | // [1, n] 约数个数 |
sieve sum of divisors
$$
sum = \prod\limits_{i = 1}^{n} \sum\limits_{j = 0}^{k_{i}} p_{i}^{j}
$$
1 | vector<int> pri; |
sieve euler function
注意到在线性筛中,每一个合数都是被最小的质因子筛掉。比如设 $p_1$ 是 $n$ 的最小质因子,$n’ = \frac{n}{p_1}$,那么线性筛的过程中 $n$ 通过 $n’ \times p_1$ 筛掉。
观察线性筛的过程,我们还需要处理两个部分,下面对 $n’ \bmod p_1$ 分情况讨论。
如果 $n’ \bmod p_1 = 0$,那么 $n’$ 包含了 $n$ 的所有质因子。
$$
\begin{aligned}
\varphi(n) & = n \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} \\
& = p_1 \times n’ \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} \\
& = p_1 \times \varphi(n’)
\end{aligned}
$$
那如果 $n’ \bmod p_1 \neq 0$ 呢,这时 $n’$ 和 $p_1$ 是互质的,根据欧拉函数性质,我们有:
$$
\begin{aligned}
\varphi(n) & = \varphi(p_1) \times \varphi(n’) \\
& = (p_1 - 1) \times \varphi(n’)
\end{aligned}
$$
1 | // [0, n] 欧拉函数 (n >= 1) |
sieve mobius
$$
\mu (n)=
\begin{cases}
1 \quad \quad \quad n = 1 \
0 \quad \quad \quad n \ 含有平方因子 \
{(-1)}^{k} \quad k \ 为 \ n \ 本质不同的质因子个数
\end{cases}
$$
1 | // [0, n] 莫比乌斯函数 |
杜教筛
求数论函数前缀和 $S(n) = \sum\limits_{i = 1}^{n} f(i)$
任意数论函数 $g$,必满足:
$$
\begin{align}
\sum\limits_{i = 1}^{n} (f * g)(i) &= \sum\limits_{i = 1}^{n} \sum\limits_{d \mid i} g(d) f(\frac{i}{d}) \
&= \sum\limits_{i = 1}^{n} \sum_{ji = 1}^{n} g(i) f(j) \
&= \sum\limits_{i = 1}^{n} \sum_{j = 1}^{\lfloor \frac{n}{i} \rfloor} g(i) f(j) \
&= \sum\limits_{i = 1}^{n} g(i) \sum_{j = 1}^{\lfloor \frac{n}{i} \rfloor} f(j) \
&= \sum\limits_{i = 1}^{n} g(i) S(\lfloor \frac{n}{i} \rfloor)
\end{align}
$$
分离出首项:$g(1)S(n) = \sum\limits_{i = 1}^{n} (f * g)(i) - \sum\limits_{i = 2}^{n} g(i) S(\lfloor \frac{n}{i} \rfloor)$
对于 $S(n)$ ,先预处理出 $S(m)$ 再计算,当 $m = n^{\frac{2}{3}}$ 时,复杂度最优 $O(n^{\frac{2}{3}})$
对于 $g$ 的构造需要能 $O(1)$ 计算 $\sum\limits_{i = 1}^{n} (f * g) (i)$ 和 $\sum\limits_{i = 1}^{n} g(i)$
求 $\sum\limits_{i = 1}^{n} \varphi(i)$
因为 $\varphi * 1 = id$ ,构造 $g = 1$
1 | constexpr int N = 1 << 20; // (2E9 1s) |
求 $S(n) = \sum_{i = 1}^{n} \mu(i)$
因为 $\mu * 1 = \varepsilon$,构造 $g = 1$
1 | constexpr int N = 1 << 20; |
Min25
求积性函数前缀和。
$$
\sum_{i = 1}^{n} = f(i)
$$
限制:
- $f(p)$ 是关于 $p$ 的项数较少的多项式或可以快速求值。
- $f(p^{c})$ 可以快速求值。
记号:
- $\Rho$ 表示全体质数集合
- $p_{i}$ 表示第 $i$ 个质数,特别的 $p_{0} = 0$
- $minp(i)$ 表示 $i$ 的最小质因子,特别的 $minp(1) = 1$
第一部分
设一个完全积性函数 $F(x)$ ,要求 $F(p) = f(p)$ 。
构造一个函数 $G(n, j) = \sum\limits_{i = 1}^{n} F(i) [i \in \Rho ~ or ~ p_{j} < minp(i)]$ 。
考虑求解函数 $G(n, j)$ :
$p_{j}^{2} > n$ 时($p_{j} > \sqrt{n}$)
$G(n, j) = G(n, j - 1)$
$p_{j}^{2} \le n$ 时($p_{j} \le \sqrt{n}$)
将 $i$ 分解成 $p_{j} \times k$,$G(n, j)$ 到 $ G(n, j - 1)$ 要加上的贡献为 $\sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(kp_{j}) [p_{j} \le minp(k)]$ 。
由于 $F(x)$ 为完全积性函数,$\sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(kp_{j}) [p_{j} \le minp(k)] = F(p_{j}) \sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(k) [p_{j} \le minp(k)]$ 。
其中 $\sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(k) [p_{j} \le minp(k)] = G(\lfloor \frac{n}{p_{j}} \rfloor, j - 1) - \sum\limits_{i = 1}^{j - 1} F(p_{i})$ 。
故 $G(n, j)$ 的递推式为:
$$
G(n, j) = \left{
\begin{align}
& G(n, j - 1) & p_{j}^{2} > n \
& G(n, j - 1) - F(p_{j}) (G(\lfloor \frac{n}{p_{j}} \rfloor, j - 1) - \sum\limits_{i = 1}^{j - 1} F(p_{i})) & otherwise
\end{align}
\right.
$$
这样就能递归求解 $G$ 。
第二部分
构造 $S(n, j) = \sum\limits_{i = 1}^{n} f(i) [p_{j} < minp(i)]$ 。
把 $i$ 分成质数和合数讨论 (1 单独算)
质数贡献:
$\sum\limits_{p \in \Rho \wedge p \le n} f(p) - \sum\limits_{i = 1}^{j} f(p_{i}) = G(n, +\infty) - \sum\limits_{i = 1}^{j} f(p_{i})$
合数贡献:
$\sum\limits_{k > j}^{+\infty} \sum\limits_{i = 1}^{p_{k}^{i} \le n} f(p_{k}^{i}) (S(\lfloor \frac{n}{p_{k}^{i}} \rfloor, k) + [i > 1])$
综上:
$$
S(n, j) = G(n, +\infty) - \sum\limits_{i = 1}^{j} f(p_{i}) + \sum\limits_{k > j}^{+\infty} \sum\limits_{i = 1}^{p_{k}^{i} \le n} f(p_{k}^{i}) (S(\lfloor \frac{n}{p_{k}^{i}} \rfloor, k) + [i > 1])
$$
$$
\sum_{i = 1}^{n} f(i) = S(n, 0) + 1
$$
1 | /* |
例如
给定 $f(p^{k}) = p^{k} (p^{k} - 1)$
拆成两部分 $f(p^{k}) = p^{2k}$ 和 $f(p^{k}) = p^{k}$ 计算差值
$f_{1}(x) = -x \quad f_2(x) = x^{2}$
1 | g1 = n * (n + 1) / 2 - 1; // 系数 -1 |

