Number theory

Inverse

$ax \equiv 1$ $(mod \quad n)$

逆元存在的充要条件 $gcd(a, n) = 1$

1. $n$ 是质数且 $gcd(a, n) = 1$，逆元 $x \equiv a^{n - 2} \quad (mod \quad n)$ （费马小定理）

2. $ax + ny = gcd(a, n)$，$gcd(a, n) = 1$ ，求 $x$ 的最小正整数解 （Exgcd 求解）

3. 线性递推 $1,2,\cdots,n$ 的逆元：$inv_{i} = (p - \lfloor \frac{p}{i} \rfloor ) \times inv_{p ; mod ; i} \quad mod ; p$

inv[1] = 1;
for (int i = 2; i <= n; ++i) {
  inv[i] = (long long)(p - p / i) * inv[p % i] % p;
}

4. 计算任意 $n$ 个数的逆元，先求前缀积 $S_{n}$ ，对 $S_{n}$ 利用 1 或 2 求解 $S_{n}$ 的逆元 $InvS_{n}$ ，则 $a_{n}$ 的逆元为 $InvS_{n} \times S_{n - 1}$， $InvS_{n - 1} = InvS_{n} \times a_{n}$ 递推即可

s[0] = 1;
for (int i = 1; i <= n; ++i) s[i] = s[i - 1] * a[i] % p;
sv[n] = qpow(s[n], p - 2); // 当然这里也可以用 exgcd 来求逆元,视个人喜好而定.
for (int i = n; i >= 1; --i) sv[i - 1] = sv[i] * a[i] % p;
for (int i = 1; i <= n; ++i) inv[i] = sv[i] * s[i - 1] % p;

Exgcd

$$
ax + by = gcd(a, b)
$$

求可行解 $x_{0}$ ，$y_{0}$ ，以下为通解
$$
x = x_{0} + \frac{b}{gcd(a, b)} k \
y = y_{0} - \frac{a}{gcd(a, b)} k
$$

long long Exgcd(long long a, long long b, long long& x, long long& y) {
	if (!b) {
		x = 1;
		y = 0;
		return a;
	}

	long long c = Exgcd(b, a % b, y, x);
	y -= (a / b) * x;
	return c;
}

Bézout’s Lemma

裴蜀定理
$$
ax + by = m
$$
有解的充要条件 $gcd(a, b) \mid m$

通解可利用 Exgcd 求
$$
x = (x_{0} + \frac{b}{gcd(a, b)} k) \frac{m}{gcd(a, b)} \
y = (y_{0} - \frac{a}{gcd(a, b)} k) \frac{m}{gcd(a, b)}
$$

Fermat’s little theorem

费马小定理

$p$ 为质数且 $gcd(a, p) = 1$ ，则 $a^{p - 1} \equiv 1 \quad (mod \quad p)$

求逆元 $ax \equiv 1 \quad (mod \quad p)$

$a \times a^{p - 2} \equiv 1 \quad (mod \quad p) \Rightarrow x \equiv a^{p - 2} \quad (mod \quad p)$

Euler’s function

$$
\varphi(n) = n \times \prod\limits_{i = 1}^{k} \frac{p_{i} - 1}{p_{i}}
$$

质因数分解计算 $O(\sqrt{n})$

long long phi(long long x) {
    long long p = x;
    for (long long i = 2; i * i <= x; i++) {
        if (x % i == 0) {
            p /= i;
            p *= i - 1;
            while (x % i == 0) {
                x /= i;
            }
        }
    }
    if (x > 1) {
        p /= x;
        p *= x - 1;
    }
    return p;
}

可用 Pollard Rho 算法优化。

$$
gcd(a, p) = 1 \Rightarrow a^{\varphi(p)} \equiv 1 \quad (mod \quad p)
$$

$n$ 的所有约数的欧拉函数值之和为 $n$
$$
\sum_{d \mid n} \varphi(d) = n
$$

trick

求 $a_{1}^{a_{2}^{\cdots}} ; % ; p $ 的值，可以递归求解，注意扩展欧拉定理的适用范围，最多进行 $\log$ 次，$\varphi(p)$ 就会变为 1，

// 查询一个区间的答案 [l, r],现预处理 phi 的值
auto dfs = [&](auto dfs, int l, int r, int dep) -> long long {
    if (l > r || vphi[dep] == 1) {
        return 1;
    }
    return quick_power(val[l], dfs(dfs, l + 1, r, dep + 1), vphi[dep]);
};
// 快速幂稍微修改一下，符合扩展欧拉定理
long long quick_power(long long a, long long b, long long p) {
    int flag = a >= p;
    a %= p;
    long long res = 1;
    while (b) {
        if (b & 1) {
            if (res * a >= p) {
                flag = 1;
            }
            res = res * a % p;
        }
        if (a * a >= p && b != 0) {
            flag = 1;
        }
        a = a * a % p;
        b >>= 1;
    }
    return res + flag * p;
}

Euler’s theorem

若 $gcd(a, p) = 1$ ，则 $a^{\varphi(p)} \equiv 1 \quad (mod \quad p) $ （$\varphi(x)$ 表示 $1$ 到 $x$ 与 $x$ 互质的数的个数）

扩展欧拉定理
$$
a^{b} \equiv
\begin{cases}
a^{b ; mod ; \varphi(p)} & gcd(a, p) = 1 \
a^{b} & gcd(a, p) \neq 1, b < \varphi(p) \
a^{(b ; mod ; \varphi(p)) + \varphi(p)} & gcd(a, p) \neq 1, b \ge \varphi(p)
\end{cases}
\quad (mod \quad p)
$$

Wilson

$(p - 1)! \equiv -1 \quad(mod \quad p)$ 是 $p$ 为质数的充分必要条件

Legendre

$n!$ 中含有的素数 $p$ 的幂次 $v_p(n!)$ 为 $\sum\limits_{i = 1}^{\infty} \lfloor \frac{n}{p^{i}} \rfloor = \frac{n - S_{p}(n)}{p - 1}$ （$S_{p}(n)$ 表示 $n$ 在 $p$ 进制下的各位数的和）

int multiplicity_factorial(int n, int p) {
  int count = 0;
  do {
    n /= p;
    count += n;
  } while (n);
  return count;
} // 计算 vp(n!)

Kummer

素数 $p$ 在组合数 $\dbinom{n}{m}$ 中的幂次，恰好是 $p$ 进制下 $m$ 减掉 $n$ 需要借位的次数。
$$
v_p\left(\dbinom{n}{m}\right)=\frac{S_p(m)+S_p(n-m)-S_p(n)}{p-1}
$$
（$S_{p}(n)$ 表示 $n$ 在 $p$ 进制下的各位数的和）

Lucas

Lucas 定理内容如下：对于质数 $p$，有

$$
\binom{n}{m}\bmod p = \binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}\cdot\binom{n\bmod p}{m\bmod p}\bmod p
$$

观察上述表达式，可知 $n\bmod p$ 和 $m\bmod p$ 一定是小于 $p$ 的数，可以直接求解，$\displaystyle\binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}$ 可以继续用 Lucas 定理求解。这也就要求 $p$ 的范围不能够太大，一般在 $10^5$ 左右。边界条件：当 $m=0$ 的时候，返回 $1$。

时间复杂度为 $O(f(p) + g(n)\log n)$，其中 $f(n)$ 为预处理组合数的复杂度，$g(n)$ 为单次求组合数的复杂度。

long long lucas(long long n, long long m) {
    if (m == 0) return 1;
    return lucas(n / mod, m / mod) * C(n % mod, m % mod) % mod;
}

exlucas

模数是个合数，

// to do

ExCrt

给定 $n$ 组非负整数 $a_i, b_i$ ，求解关于 $x$ 的方程组的最小非负整数解。
$$
\begin{cases}
x\equiv b_1\pmod{a_1}\
x\equiv b_2\pmod{a_2}\
\dots\
x\equiv b_n\pmod{a_n}
\end{cases}
$$
采用裴蜀定理计算求得通解，逐个合并求解，通解：$x_{0} + k \times mod$

设两个方程分别是 $x\equiv a_1 \pmod {m_1}$、$x\equiv a_2 \pmod {m_2}$；

将它们转化为不定方程：$x=m_1p+a_1=m_2q+a_2$，其中 $p, q$ 是整数，则有 $m_1p-m_2q=a_2-a_1$。

由裴蜀定理，当 $a_2-a_1$ 不能被 $\gcd(m_1,m_2)$ 整除时，无解；

其他情况下，可以通过扩展欧几里得算法解出来一组可行解 $(p, q)$；

则原来的两方程组成的模方程组的解为 $x\equiv b\pmod M$，其中 $b=m_1p+a_1$，$M=\text{lcm}(m_1, m_2)$。

多个方程用上面的方法两两合并即可。

template<class T = __int128_t>
struct ExCrt {
    vector<pair<T, T>> EquationSet;

    ExCrt() {}
    // remain 和 mod 都是非负整数
    void insert(const T& remain, const T& mod) {
        EquationSet.push_back({ remain, mod });
    }

    T ExGcd(T a, T b, T& x, T& y) {
        if (b == 0) {
            x = 1;
            y = 0;
            return a;
        }
        T c = ExGcd(b, a % b, y, x);
        y -= (a / b) * x;
        return c;
    }

    T get(const T& val, const T& mod) { // 返回同余最小非负整数
        T res = val % mod;
        if (res < 0) {
            res += mod;
        }
        return res;
    }
    // 求同余的最小非负整数 无解返回 -1
    T work() {
        T result = 0;
        T mod = 1;
        T x, y, r, g;
        for (auto& [a, m] : EquationSet) {
            r = get(a - result, m);
            g = ExGcd(mod, m, x, y);
            if (r % g != 0) { // 裴蜀定理
                return -1; // 无解
            }
            x = x * (r / g) % (m / g);
            result += x * mod;
            mod *= (m / g);
            result = get(result, mod);
        }
        return result;
    }

    void reset() {
        EquationSet.clear();
    }
};

ExBSGS

求满足 $a^{x} \equiv b \quad (mod \quad p)$ 的最小非负整数解

考虑分块 $x = i \times m - j$ 先枚举 $j$ 把结果放到哈希表中，再枚举 $i$ 查找结果（ $m = \sqrt{p}$ ）

$a < m, b < m$ 不满足就先 $mod$ 一下。

对 $a,b,m\in\mathbf{Z}^+$，求解

$$
a^x\equiv b\pmod m
$$

其中 $a,m$ 不一定互质。

当 $(a, m)=1$ 时，在模 $m$ 意义下 $a$ 存在逆元，因此可以使用 BSGS 算法求解。于是我们想办法让他们变得互质。

具体地，设 $d_1=(a, m)$. 如果 $d_1\nmid b$，则原方程无解。否则我们把方程同时除以 $d_1$，得到

$$
\frac{a}{d_1}\cdot a^{x-1}\equiv \frac{b}{d_1}\pmod{\frac{m}{d_1}}
$$

如果 $a$ 和 $\frac{m}{d_1}$ 仍不互质就再除，设 $d_2=\left(a, \frac{m}{d_1}\right)$. 如果 $d_2\nmid \frac{b}{d_1}$，则方程无解；否则同时除以 $d_2$ 得到

$$
\frac{a^2}{d_1d_2}\cdot a^{x-2}≡\frac{b}{d_1d_2} \pmod{\frac{m}{d_1d_2}}
$$

同理，这样不停的判断下去，直到 $a\perp \dfrac{m}{d_1d_2\cdots d_k}$.

记 $D=\prod_{i=1}^kd_i$，于是方程就变成了这样：

$$
\frac{a^k}{D}\cdot a^{x-k}\equiv\frac{b}{D} \pmod{\frac{m}{D}}
$$

由于 $a\perp\dfrac{m}{D}$，于是推出 $\dfrac{a^k}{D}\perp \dfrac{m}{D}$. 这样 $\dfrac{a^k}{D}$ 就有逆元了，于是把它丢到方程右边，这就是一个普通的 BSGS 问题了，于是求解 $x-k$ 后再加上 $k$ 就是原方程的解啦。

注意，不排除解小于等于 $k$ 的情况，所以在消因子之前做一下 $\Theta(k)$ 枚举，直接验证 $a^i\equiv b \pmod m$，这样就能避免这种情况。

template<class T = long long>
T quick_power(T a, T b, T p) {
    a %= p;
    T res = 1;
    while (b != 0) {
        if (b % 2 == 1) {
            res = res * a % p;
        }
        a = a * a % p;
        b /= 2;
    }
    return res;
}

template<class T = long long>
T ExBSGS(T a, T b, T p) {
    a %= p;
    b %= p;
    if (b == 1 || p == 1) {
        return 0;
    }
    T g, k = 0, A = 1;
    while (true) { // 使 a, p 互质
        g = gcd(a, p);
        if (g == 1) { // 已经互质
            break;
        }
        if (b % g != 0) {
            return -1; // 无解
        }
        b /= g;
        p /= g;
        k += 1;
        A = A * (a / g) % p;
        if (A == b) {
            return k;
        }
    }
    T m = sqrt(p) + 1; // 分块
    unordered_map<T, T> f;
    f[b] = 0;
    T t = b;
    for (T j = 1; j < m; j++) {
        t = t * a % p;
        f[t] = j;
    }
    T mi = quick_power(a, m, p);
    t = A; // 更改 t 
    for (T i = 1; i <= m; i++) {
        t = t * mi % p;
        if (f.count(t)) {
            return i * m - f[t] + k;
        }
    }
    return -1;
}

BSGS

long long quick_power(long long a, long long b, long long p){
    a %= p;
    long long res = 1;
    while(b){
        if(b & 1){
            res = res * a % p;
        }
        a = a * a % p;
        b >>= 1;
    }
    return res;
}

// p 为 质数
long long BSGS(long long a, long long b, long long p) {
    a %= p;
    b %= p;
    if (b == 1 && p == 1) {
        return 0;
    }

    long long m = sqrt(p) + 1;
    unordered_map<long long, long long> f;
    f[b] = 0;
    long long t = b;
    for (long long i = 1; i < m; i++) {
        t = t * a % p;
        f[t] = i;
    }

    long long am = quick_power(a, m, p);
    t = 1;
    for (long long i = 1; i <= m; i++) {
        t = t * am % p;
        if (f.count(t)) {
            return i * m - f[t];
        }
    }
    return -1;
}

Primitive-root

满足同余式 $a^n \equiv 1 \pmod m$ 的最小正整数 $n$ 存在，这个 $n$ 称作 $a$ 模 $m$ 的阶，记作 $\delta_m(a)$ 或 $\operatorname{ord}_m(a)$.

性质

1. $a,a^2,\cdots,a^{\delta_m(a)}$ 模 $m$ 两两不同余。
2. 若 $a^n \equiv 1 \pmod m$，则 $\delta_m(a)\mid n$.
3. 设 $m\in\mathbf{N}^{*}$，$a,b\in\mathbf{Z}$，$(a,m)=(b,m)=1$，则 $\delta_m(ab)=\delta_m(a)\delta_m(b)$ 的充分必要条件是 $\left(\delta_m(a), \delta_m(b)\right)=1$
4. 设 $k \in \mathbf{N}$，$m\in \mathbf{N}^{*}$，$a\in\mathbf{Z}$，$(a,m)=1$，则 $\delta_m(a^k)=\dfrac{\delta_m(a)}{\left(\delta_m(a),k\right)}$

设 $m \in \mathbf{N}^{}$，$g\in \mathbf{Z}$. 若 $(g,m)=1$，且 $\delta_m(g)=\varphi(m)$，则称 $g$ 为模 $m$ 的原根。
即 $g$ 满足 $\delta_m(g) = \left| \mathbf{Z}_m^ \right| = \varphi(m)$. 当 $m$ 是质数时，我们有 $g^i \bmod m,,0 \lt i \lt m$ 的结果互不相同。

原根判定定理

设 $m \geqslant 3, (g,m)=1$，则 $g$ 是模 $m$ 的原根的充要条件是，对于 $\varphi(m)$ 的每个素因数 $p$，都有 $g^{\frac{\varphi(m)}{p}}\not\equiv 1\pmod m$.

// 如果有原根，在 p^0.25 就能找到 复杂度 (p^0.25 * log(phi(p))) 最小原根
auto findPrimitiveRoot = [&](long long p) -> long long {
    auto factors = factorize(phi[p]);
    for (long long i = 1; i < p; i++) {
        if (power(i, phi[p], p) == 1) {
            bool flag = true;
            for (auto f : factors) { // phi[p] 的所有因子
                if (power(i, phi[p] / f, p) == 1) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                return i;
            }
        }
    }
    return 0;
};

原根存在定理

一个数 $m$ 存在原根当且仅当 $m=2,4,p^{\alpha},2p^{\alpha}$，其中 $p$ 为奇素数，$\alpha\in \mathbf{N}^{*}$.

// 判断 [0, n] 内的数有无 primitive root (n >= 4) 
// 有原根的类型 2, 4, p^a, 2*p^a (p 为奇质数)
auto haveRoot = [&](long long n) -> vector<int> {
    vector<int> have(n + 1);
    have[2] = true;
    have[4] = true;
    for (int i = 1; i < primes.size(); i++) { // p^a, 2*p^a 都有原根 (p 为奇质数)
        long long cur = primes[i];
        while (cur <= n) {
            have[cur] = true;
            if (cur * 2 <= n) {
                have[cur * 2] = true;
            }
            cur *= primes[i];
        }
    }
    return have;
};
auto have = haveRoot(N);

原根个数

若一个数 $m$ 有原根，则它原根的个数为 $\varphi(\varphi(m))$.

// phi(p) * log(p) 时间算所有原根 最小原根 g ，所有原根 g^k % p (gcd(k, phi(p)) == 1)
auto allPrimitiveRoot = [&](long long p) -> vector<int> {
    auto rt = findPrimitiveRoot(p);
    vector<int> root;
    root.push_back(rt);
    long long x = rt;
    for (int i = 2; i < phi[p]; i++) {
        x = x * rt % p;
        if (gcd(i, phi[p]) == 1) {
            root.push_back(x);
        }
    }
    sort(root.begin(), root.end());
    return root;
};
// 最终 phi(phi(p)) 个

Sqrt-decomposition

引理
$$
\forall a,b,c\in\mathbb{Z},\left\lfloor\frac{a}{bc}\right\rfloor=\left\lfloor\frac{\left\lfloor\frac{a}{b}\right\rfloor}{c}\right\rfloor
$$

结论

对于常数 $n$，使得式子
$$
\left\lfloor\dfrac ni\right\rfloor=\left\lfloor\dfrac nj\right\rfloor
$$

成立且满足 $i\leq j\leq n$ 的 $j$ 值最大为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$，即值 $\left\lfloor\dfrac ni\right\rfloor$ 所在块的右端点为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$。

（$i$ 不是第几块，而是下标）

向上取整

向上取整与前文所述的向下取整十分类似，但略有区别：

对于常数 $n$，使得式子

$$
\left\lceil\dfrac ni\right\rceil=\left\lceil\dfrac nj\right\rceil
$$

成立且满足 $i\leq j\leq n$ 的 $j$ 值最大为 $\left\lfloor\dfrac{n-1}{\lfloor\frac{n-1}i\rfloor}\right\rfloor$，即值 $\left\lceil\dfrac ni\right\rceil$ 所在块的右端点为 $\left\lfloor\dfrac{n-1}{\lfloor\frac{n-1}i\rfloor}\right\rfloor$。

当 $i=n$ 时，上式会出现分母为 $0$ 的错误，需要特殊处理。

证明：$\left\lceil\dfrac ni\right\rceil=\left\lfloor\dfrac{n-1}i\right\rfloor+1$，可以发现 $n$ 的上取整分块与 $n-1$ 的下取整分块是一样的。

Mobius

$$
f(n) = \sum\limits_{d \mid n} g(d) \
g(n) = \sum\limits_{d \mid n} \mu(d) f(\frac{n}{d})
$$

数论函数 $f(n)$ 称为数论函数 $g(n)$ 的莫比乌斯变换

数论函数 $g(n)$ 称为数论函数 $f(n)$ 的莫比乌斯逆变换（反演）

反演结论：
$$
\sum\limits_{d \mid gcd(i, j)} \mu(d) = [gcd(i, j) = 1]
$$

Linear sieves

sieve primes

每个质数被其最小的因子删除

// [2, n] 内的质数
vector<int> linear_sieves(int n){
    vector<int> res;
    vector<int> vis(n + 1);
    for(long long i = 2; i <= n; i++){
        if(!vis[i]){
            res.push_back(i);
        }

        for(long long j = 0; j < res.size() && i * res[j] <= n; j++){
            vis[i * res[j]] = true;
            if(i % res[j] == 0){
                break;
            }
        }
    }
    return res;
}

sieve divisors

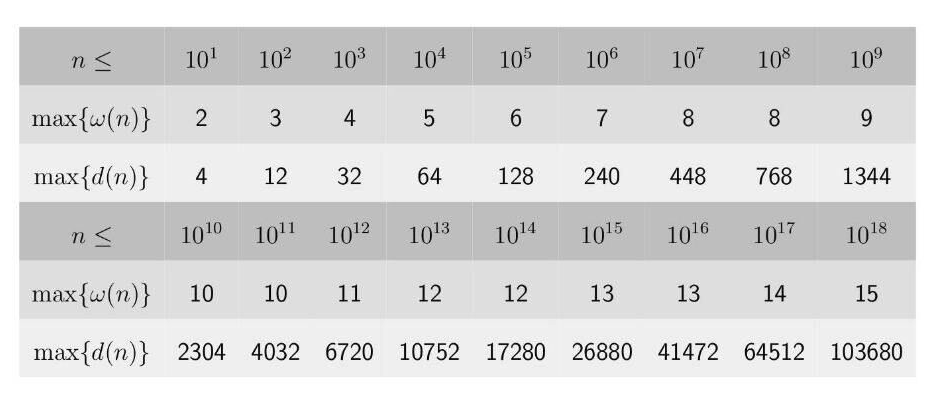
$w(n)$ 表示质因子最多的个数

$d(n)$ 表示约数最多的个数

// 求 [0, n) 某个数的约数 
struct Divisor {
    vector<int> p, v;
    Divisor(int n) {
        v.resize(n);
        for (long long i = 2; i < n; i++) {
            if (!v[i]) {
                v[i] = i;
                p.push_back(i);
            }

            for (int j = 0; j < p.size() && i * p[j] < n; j++) {
                v[i * p[j]] = p[j];
                if (i % p[j] == 0) {
                    break;
                }
            }
        }
    }

    auto get(int x) const {
        vector<int> div(1, 1);
        while (x > 1) {
            int l = 0;
            int r = div.size();
            int d = v[x];
            while (x % d == 0) {
                for (int i = l; i < r; i++) {
                    div.push_back(div[i] * d);
                }
                x /= d;
                l = r;
                r = div.size();
            }
        }
        return div; 
    }
};

sieve count of divisors

$$
唯一分解定理 \quad x = \prod_{i = 1}^{n} p_{i}^{k_{i}} \quad
$$

$$
乘法原理 \quad 约数个数 = \prod_{i = 1}^{n}(k_{i} + 1)
$$

// [1, n] 约数个数
vector<int> sieve_divisors(int n) {
    vector<int> primes;
    vector<int> cnt(n + 1, 1), p(n + 1), vis(n + 1);
    for (long long i = 2; i <= n; i++) {
        if (!vis[i]) {
            primes.push_back(i);
            cnt[i] = 2;
            p[i] = 1;
        }

        for (int j = 0; j < primes.size() && i * primes[j] <= n; j++) {
            int val = i * primes[j];
            vis[val] = true;
            if (i % primes[j] == 0) {
                p[val] = p[i] + 1;
                cnt[val] = cnt[i] / (p[i] + 1) * (p[val] + 1);
                break;
            } else {
                p[val] = 1;
                cnt[val] = cnt[i] * (p[val] + 1);
            }
        }
    }
    return cnt;
}

sieve sum of divisors

$$
sum = \prod\limits_{i = 1}^{n} \sum\limits_{j = 0}^{k_{i}} p_{i}^{j}
$$

vector<int> pri;
bool not_prime[N];
int g[N], f[N];

void pre(int n) {
  g[1] = f[1] = 1;
  for (int i = 2; i <= n; ++i) {
    if (!not_prime[i]) {
      pri.push_back(i);
      g[i] = i + 1;
      f[i] = i + 1;
    }
    for (int pri_j : pri) {
      if (i * pri_j > n) break;
      not_prime[i * pri_j] = true;
      if (i % pri_j == 0) {
        g[i * pri_j] = g[i] * pri_j + 1;
        f[i * pri_j] = f[i] / g[i] * g[i * pri_j];
        break;
      }
      f[i * pri_j] = f[i] * f[pri_j];
      g[i * pri_j] = 1 + pri_j;
    }
  }
}

sieve euler function

注意到在线性筛中，每一个合数都是被最小的质因子筛掉。比如设 $p_1$ 是 $n$ 的最小质因子，$n’ = \frac{n}{p_1}$，那么线性筛的过程中 $n$ 通过 $n’ \times p_1$ 筛掉。

观察线性筛的过程，我们还需要处理两个部分，下面对 $n’ \bmod p_1$ 分情况讨论。

如果 $n’ \bmod p_1 = 0$，那么 $n’$ 包含了 $n$ 的所有质因子。

$$
\begin{aligned}
\varphi(n) & = n \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} \\
& = p_1 \times n’ \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} \\
& = p_1 \times \varphi(n’)
\end{aligned}
$$

那如果 $n’ \bmod p_1 \neq 0$ 呢，这时 $n’$ 和 $p_1$ 是互质的，根据欧拉函数性质，我们有：

$$
\begin{aligned}
\varphi(n) & = \varphi(p_1) \times \varphi(n’) \\
& = (p_1 - 1) \times \varphi(n’)
\end{aligned}
$$

// [0, n] 欧拉函数 (n >= 1)
vector<int> sieve_euler_func(long long n) {
    vector<int> phi(n + 1), primes;
    phi[1] = 1;
    for (long long i = 2; i <= n; i++) {
        if (!phi[i]) {
            phi[i] = i - 1;
            primes.push_back(i);
        }
        for (auto& p : primes) {
            if (i * p > n) {
                break;
            }
            if (i % p == 0) {
                phi[i * p] = phi[i] * p;
                break;
            }
            phi[i * p] = phi[i] * phi[p];
        }
    }
    return phi;
};

sieve mobius

$$
\mu (n)=
\begin{cases}
1 \quad \quad \quad n = 1 \
0 \quad \quad \quad n \ 含有平方因子 \
{(-1)}^{k} \quad k \ 为 \ n \ 本质不同的质因子个数
\end{cases}
$$

// [0, n] 莫比乌斯函数
vector<int> mobius(int n) {
    vector<int> mu(n + 1), vis(n + 1), primes;
    mu[1] = 1;
    for (long long i = 2; i <= n; i++) {
        if (!vis[i]) {
            mu[i] = -1;
            vis[i] = true;
            primes.push_back(i);
        }
        for (auto& p : primes) {
            if (i * p > n) {
                break;
            }
            vis[i * p] = true;
            if (i % p == 0) {
                mu[i * p] = 0;
                break;
            }
            mu[i * p] = -mu[i];
        }
    }
    return mu;
}

杜教筛

求数论函数前缀和 $S(n) = \sum\limits_{i = 1}^{n} f(i)$

任意数论函数 $g$，必满足：
$$
\begin{align}
\sum\limits_{i = 1}^{n} (f * g)(i) &= \sum\limits_{i = 1}^{n} \sum\limits_{d \mid i} g(d) f(\frac{i}{d}) \
&= \sum\limits_{i = 1}^{n} \sum_{ji = 1}^{n} g(i) f(j) \
&= \sum\limits_{i = 1}^{n} \sum_{j = 1}^{\lfloor \frac{n}{i} \rfloor} g(i) f(j) \
&= \sum\limits_{i = 1}^{n} g(i) \sum_{j = 1}^{\lfloor \frac{n}{i} \rfloor} f(j) \
&= \sum\limits_{i = 1}^{n} g(i) S(\lfloor \frac{n}{i} \rfloor)
\end{align}
$$
分离出首项：$g(1)S(n) = \sum\limits_{i = 1}^{n} (f * g)(i) - \sum\limits_{i = 2}^{n} g(i) S(\lfloor \frac{n}{i} \rfloor)$

对于 $S(n)$ ，先预处理出 $S(m)$ 再计算，当 $m = n^{\frac{2}{3}}$ 时，复杂度最优 $O(n^{\frac{2}{3}})$

对于 $g$ 的构造需要能 $O(1)$ 计算 $\sum\limits_{i = 1}^{n} (f * g) (i)$ 和 $\sum\limits_{i = 1}^{n} g(i)$

求 $\sum\limits_{i = 1}^{n} \varphi(i)$

因为 $\varphi * 1 = id$ ，构造 $g = 1$

constexpr int N = 1 << 20; // (2E9 1s)

vector<int> phi;
vector<long long> sphi;
unordered_map<long long, long long> fphi;

phi = euler(N);
sphi.assign(N + 1, 0);
for (int i = 1; i <= N; i++) {
    sphi[i] = sphi[i - 1] + phi[i];
}

long long getSphi(long long n) {
    if (n <= N) {
        return sphi[n];
    }
    if (fphi.count(n)) { // 记忆化
        return fphi[n];
    }
    long long res = n * (n + 1) / 2;
    for (long long l = 2, r = 2; l <= n; l = r + 1) {
        r = n / (n / l);
        res -= (r - l + 1) * getSphi(n / l);
    }
    return fphi[n] = res;
}

求 $S(n) = \sum_{i = 1}^{n} \mu(i)$

因为 $\mu * 1 = \varepsilon$，构造 $g = 1$

constexpr int N = 1 << 20;

vector<int> mu;
vector<long long> smu;
unordered_map<long long, long long> fmu;

mu = mobius(N);
smu.assign(N + 1, 0);
for (int i = 1; i <= N; i++) {
    smu[i] = smu[i - 1] + mu[i];
}

long long getSmu(long long n) {
    if (n <= N) {
        return smu[n];
    }
    if (fmu.count(n)) {
        return fmu[n];
    }
    long long res = 1; // 单位元前缀和 1  !!!
    for (long long l = 2, r = 2; l <= n; l = r + 1) {
        r = n / (n / l);
        res -= (r - l + 1) * getSmu(n / l);
    }
    return fmu[n] = res;
}

Min25

求积性函数前缀和。
$$
\sum_{i = 1}^{n} = f(i)
$$
限制：

1. $f(p)$ 是关于 $p$ 的项数较少的多项式或可以快速求值。
2. $f(p^{c})$ 可以快速求值。

记号：

1. $\Rho$ 表示全体质数集合
2. $p_{i}$ 表示第 $i$ 个质数，特别的 $p_{0} = 0$
3. $minp(i)$ 表示 $i$ 的最小质因子，特别的 $minp(1) = 1$

第一部分

设一个完全积性函数 $F(x)$ ，要求 $F(p) = f(p)$ 。

构造一个函数 $G(n, j) = \sum\limits_{i = 1}^{n} F(i) [i \in \Rho ~ or ~ p_{j} < minp(i)]$ 。

考虑求解函数 $G(n, j)$ ：

1. $p_{j}^{2} > n$ 时（$p_{j} > \sqrt{n}$）

   $G(n, j) = G(n, j - 1)$

2. $p_{j}^{2} \le n$ 时（$p_{j} \le \sqrt{n}$）

将 $i$ 分解成 $p_{j} \times k$，$G(n, j)$ 到 $ G(n, j - 1)$ 要加上的贡献为 $\sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(kp_{j}) [p_{j} \le minp(k)]$ 。

由于 $F(x)$ 为完全积性函数，$\sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(kp_{j}) [p_{j} \le minp(k)] = F(p_{j}) \sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(k) [p_{j} \le minp(k)]$ 。

其中 $\sum\limits_{k = p_{j}}^{\lfloor \frac{n}{p_{j}} \rfloor} F(k) [p_{j} \le minp(k)] = G(\lfloor \frac{n}{p_{j}} \rfloor, j - 1) - \sum\limits_{i = 1}^{j - 1} F(p_{i})$ 。

故 $G(n, j)$ 的递推式为：
$$
G(n, j) = \left{
\begin{align}
& G(n, j - 1) & p_{j}^{2} > n \
& G(n, j - 1) - F(p_{j}) (G(\lfloor \frac{n}{p_{j}} \rfloor, j - 1) - \sum\limits_{i = 1}^{j - 1} F(p_{i})) & otherwise
\end{align}
\right.
$$
这样就能递归求解 $G$ 。

第二部分

构造 $S(n, j) = \sum\limits_{i = 1}^{n} f(i) [p_{j} < minp(i)]$ 。

把 $i$ 分成质数和合数讨论 (1 单独算)

质数贡献：

$\sum\limits_{p \in \Rho \wedge p \le n} f(p) - \sum\limits_{i = 1}^{j} f(p_{i}) = G(n, +\infty) - \sum\limits_{i = 1}^{j} f(p_{i})$

合数贡献：

$\sum\limits_{k > j}^{+\infty} \sum\limits_{i = 1}^{p_{k}^{i} \le n} f(p_{k}^{i}) (S(\lfloor \frac{n}{p_{k}^{i}} \rfloor, k) + [i > 1])$

综上：
$$
S(n, j) = G(n, +\infty) - \sum\limits_{i = 1}^{j} f(p_{i}) + \sum\limits_{k > j}^{+\infty} \sum\limits_{i = 1}^{p_{k}^{i} \le n} f(p_{k}^{i}) (S(\lfloor \frac{n}{p_{k}^{i}} \rfloor, k) + [i > 1])
$$

$$
\sum_{i = 1}^{n} f(i) = S(n, 0) + 1
$$

/*
    求一个多项式的前缀和 poly f = a_0 + a_1 * x + ... + a_n * x_n
    每一项分开单独求
    f(p) = a * p^{k} => f'(p) = p^{k}
    拆系数，最后结果乘 a 即可
    对于 p^{k} 需要求 \sum\limits_{i = 2}^{n} i^{k}
*/
using i64 = int64_t;

i64 n;
cin >> n;
i64 lim = sqrt(n * 4);
vector<i64> p = { 0 };
vector<i64> vis(lim + 1);
for (i64 i = 2; i <= lim; i++) {
    if (!vis[i]) {
        p.push_back(i);
    }
    for (i64 j = 1; j < p.size() && i * p[j] <= lim; j++) {
        vis[i * p[j]] = true;
        if (i % p[j] == 0) {
            break;
        }
    }
}
vector<i64> pos(lim + 1, 0);
vector<i64> idxless(lim + 1, 0);
vector<i64> idxgreater(lim + 1, 0);
vector<i64> g0(lim + 1, 0); // 0 次项 ，1 次 ... k 次
for (i64 l = 1, r, i = 1; l <= n; l = r + 1, i++) {
    pos[i] = n / l;
    if (pos[i] <= lim) {
        idxless[pos[i]] = i;
    } else {
        idxgreater[n / pos[i]] = i;
    }
    r = n / (n / l);
    // 这里计算 \sum\limits_{i = 2}^{n / l} i^{k}
    g0[i] = pos[i] - 1;
    /*
    gk[i] = \sum\limits_{i = 2}^{n / l} i^{k}; (伯努利数)
    */
}

auto idx = [&](i64 x) -> i64 {
    return x <= lim ? idxless[x] : idxgreater[n / x];
};

for (i64 j = 1; j < p.size(); j++) {
    for (i64 i = 1; i <= lim && p[j] * p[j] <= pos[i]; i++) {
        g0[i] -= power(p[j], 0) * (g0[idx(pos[i] / p[j])] - g0[idx(p[j - 1])]);
        /*
        gk[i] -= power(p[j], k) * (gk[idx(pos[i] / p[j])] - gk[idx(p[j - 1])]);
        */
    }
}

// f(p^{k}) 求解
auto f = [&](i64 p, i64 k) -> i64 {
    return /* to fill*/;
};

auto sum = [&](auto sum, i64 n, i64 c) -> i64 {
    if (p[c] >= n) {
        return 0;
    }
    i64 res = 0;
    res += a0 * (g0[idx(n)] - g0[idx(p[c])]);
    /*
    res += ak * (gk[idx(n)] - gk[idx(p[c])]); // ak 为 所求多项式系数
    */
    for (i64 i = c + 1; i < p.size() && p[i] * p[i] <= n; i++) {
        for (i64 j = 1, x = p[i]; x * p[i] <= n; j++, x *= p[i]) {
            res += f(x, j) * sum(sum, n / x, i) + f(x * p[i], j + 1);
        }
    }
    return res;
};
// ans = sum(sum, n, 0) + 1;

例如

给定 $f(p^{k}) = p^{k} (p^{k} - 1)$

拆成两部分 $f(p^{k}) = p^{2k}$ 和 $f(p^{k}) = p^{k}$ 计算差值

$f_{1}(x) = -x \quad f_2(x) = x^{2}$

g1 = n * (n + 1) / 2 - 1; // 系数 -1
g2 = n * (n + 1) * (n * 2 + 1) / 2 - 1; // 系数 1
// 系数在求 sum 处乘